Persamaan diferensial parsial
Dari Wikipedia bahasa Indonesia, ensiklopedia bebas
Persamaan diferensial parsial (PDP) adalah persamaan yang di dalamnya terdapat suku-suku
diferensial parsial, yang dalam
matematika diartikan sebagai suatu hubungan yang mengaitkan suatu
fungsi yang tidak diketahui, yang merupakan fungsi dari beberapa
variabel bebas,
dengan turunan-turunannya melalui variabel-variabel yang dimaksud. PDP
digunakan untuk melakukan formulasi dan menyelesaikan permasalahan yang
melibatkan fungsi-fungsi yang tidak diketahui, yang merupakan dibentuk
oleh beberapa variabel, seperti penjalaran
suara dan
panas,
elektrostatika,
elektrodinamika, aliran
fluida,
elastisitas, atau lebih umum segala macam proses yang terdistribusi dalam
ruang, atau terdistribusi dalam ruang dan
waktu. Kadang beberapa permasalahan fisis yang amat berbeda memiliki
formulasi matematika yang mirip satu sama lain.
Pengantar
Bentuk paling sederhana dari persamaan diferensial adalah
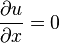
di mana
u suatu fungsi tak diketahui dari
x dan
y. Hubungan ini mengisyaratkan bahwa nilai-nilai
u(
x,
y) adalah tidak bergantung dari
x. Oleh karena itu solusi umum dari persamaan ini adalah

di mana
f adalah suatu fungsi sembarang dari variabel
y. Analogi dari
persamaan diferensial biasa untuk persamaan ini adalah

yang memiliki solusi

di mana
c bernilai konstan (tidak bergantung dari nilai
x).
Kedua contoh di atas menggambarkan bahwa solusi umum dari persamaan
diferensial biasa melibatkan suatu kostanta sembarang, akan tetapi
solusi dari persamaan diferensial parsial melibatkan suatu fungsi
sembarang. Sebuah solusi dari persamaan diferensial parsial secara umum
tidak unik; kondisi tambahan harus disertakan lebih lanjut pada
syarat batas dari daerah di mana solusi didefinisikan. Sebagai gambaran dalam contoh sederhana di atas, fungsi

dapat ditentukan jika

dispesifikasikan pada sebuah garis
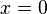
.
 dapat ditentukan jika
dapat ditentukan jika  dispesifikasikan pada sebuah garis
dispesifikasikan pada sebuah garis 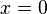 .
.
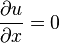



 dapat ditentukan jika
dapat ditentukan jika  dispesifikasikan pada sebuah garis
dispesifikasikan pada sebuah garis 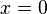 .
.

0 komentar:
Posting Komentar