Logaritma
1). Jika a dan b bilangan positif dengan 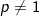 maka berlaku :
maka berlaku :
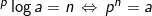
Dari hubungan tersebut, diperoleh :

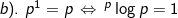

2). Sifat-sifat logaritma
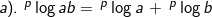
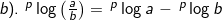
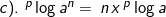
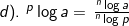
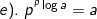
Dari hubungan tersebut, diperoleh :
2). Sifat-sifat logaritma
C. FUNGSI PERSAMAAN KUADRAT
Bentuk Umum Persamaan Kuadrat seperti ini
 ,
,  dan a, b, c,
dan a, b, c,
Dimana :
x adalah variabel persamaan kuadrat
a adalah koefisien x kuadrat
b adalah koefisien x
c adalah konstanta
 ,
,  dan a, b, c,
dan a, b, c,
Dimana :
x adalah variabel persamaan kuadrat
a adalah koefisien x kuadrat
b adalah koefisien x
c adalah konstanta
Cara Menyelesaikan Persamaan Kuadrat
1) Mencari faktor

diuraikan menjadi
cara pemfaktoran akan lebih mudah bila a = 1
maka kita bisa menebak x1 dan x2 dengan cara
a = 1
b = x1+x2
c = x1.x2
2) Memakai Rumus Kuadrat atau Rumus abc

3) Melengkapkan Kuadrat Sempurna
Bentuk umum persamaan kuadrat bebentuk kuadrat sempurna adalah :
dengan q > 0
Menentukan Jenis Akar-Akar Persamaan Kuadrat Jenis akar-akar persamaan kuadrat ditentukan oleh nilai deskriminan :

a. D > 0 Kedua akar nyata dan berlainan,
b. D = 0
Kedua akar nyata dan sama,
c. D <> Kedua akar tidak nyata (imaginer)
d.dengan

bilangan kuadrat sempurna, kedua akar rasional.
Untuk menghitung jumlah dan hasil kali akar-akar persamaan kuadrat , dapat dicari tanpa terlebih dahulu mencari akar-akarnya.
Dari rumusdan

Dapat ditunjukkan bahwa:
Rumus-rumus Akar Persamaan Kuadrat hasil pengembangan, sering sekali muncul di soal UAN SNMPTN atau SPMB
Sifat-sifat Akar Persamaan Kuadrat Jika  dan
dan  adalah akar-akar persamaan kuadrat
adalah akar-akar persamaan kuadrat  dengan
dengan 
 dan
dan  adalah akar-akar persamaan kuadrat
adalah akar-akar persamaan kuadrat  dengan
dengan 
maka berlaku sifat-sifat berikut ini :
a. Syarat mempunyai Dua Akar Positif

b. Syarat mempunyai Dua Akar Negatif

c. Syarat mempunyai Dua Akar Berlainan Tanda

d. Syarat mempunyai Dua Akar Berlawanan

e. Syarat mempunyai kedua akar berkebalikan



















0 komentar:
Posting Komentar